Bạn có biết rằng trong các kiến thức toán học, khái niệm về trọng tâm là một trong những thứ quan trọng nhất không? Thật đúng vậy! Trọng tâm được áp dụng rộng rãi trong cuộc sống hàng ngày của chúng ta. Vậy hôm nay, chúng ta cùng đi khám phá về trọng tâm và cách xác định trọng tâm một cách đơn giản và dễ hiểu nhất nhé.
Trọng tâm là gì? Trọng tâm trong toán học là gì?
- Trọng tâm có thể hiểu là một vị trí ở giữa của một cái gì đó.
- Trong toán học, trọng tâm là điểm giao nhau của ba đường trung tuyến của tam giác được hình thành từ ba đỉnh của tam giác đó.
- Trọng tâm có nhiều định nghĩa khác nhau trong nhiều lĩnh vực như trong tâm của tam giác, trọng tâm của tứ giác, trọng tâm của ngôi nhà, trọng tâm của con đường, trọng tâm của vấn đề, và cả trọng tâm trong vật lý…
Trọng tâm trong tam giác là gì?
- Trong một tam giác, trọng tâm là điểm giao nhau của ba đường trung tuyến xuất phát từ ba đỉnh của tam giác và kết thúc tại trung điểm của cạnh đối diện.
- Điểm giao nhau của ba đường trung tuyến chính là trọng tâm của tam giác.
Tính chất trọng tâm của các hình học
Trọng tâm của tam giác
- Khoảng cách từ trọng tâm của tam giác đến đỉnh bằng 2/3 độ dài đường trung tuyến tương ứng với đỉnh đó.
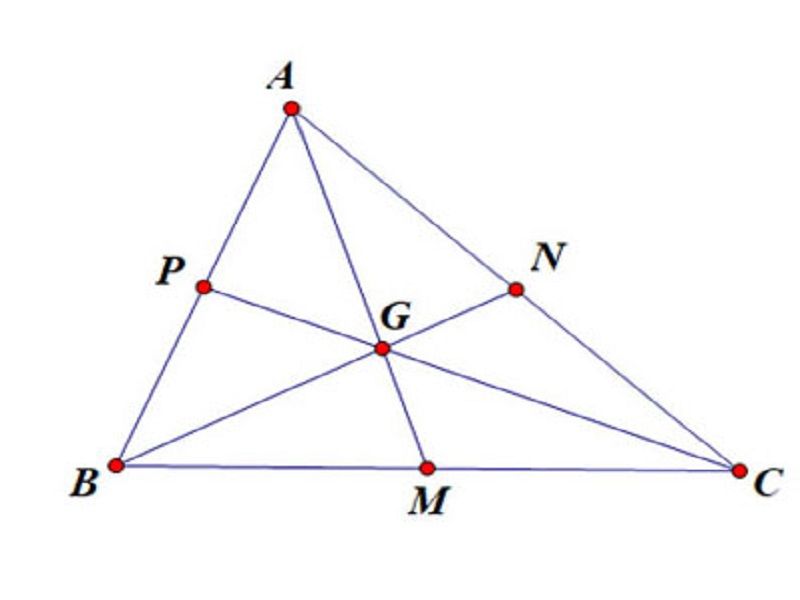
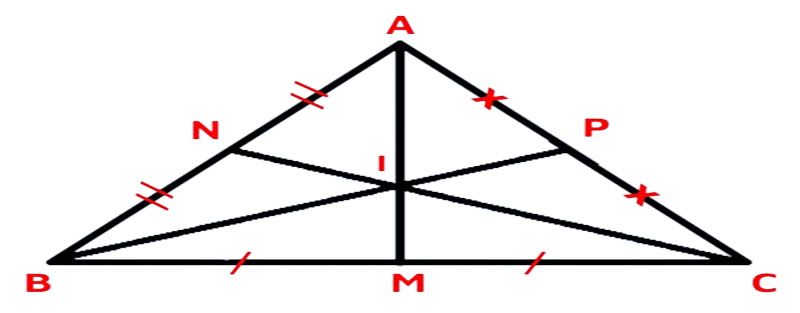
- Ví dụ: Trong tam giác ABC với các đường trung tuyến AM, BN, CP và trọng tâm G, ta có:
- GA = 2/3 AM
- GB = 2/3 BN
- GC = 2/3 CP
Trọng tâm của tam giác cân
- Trọng tâm của tam giác cân nằm tại đỉnh của tam giác.
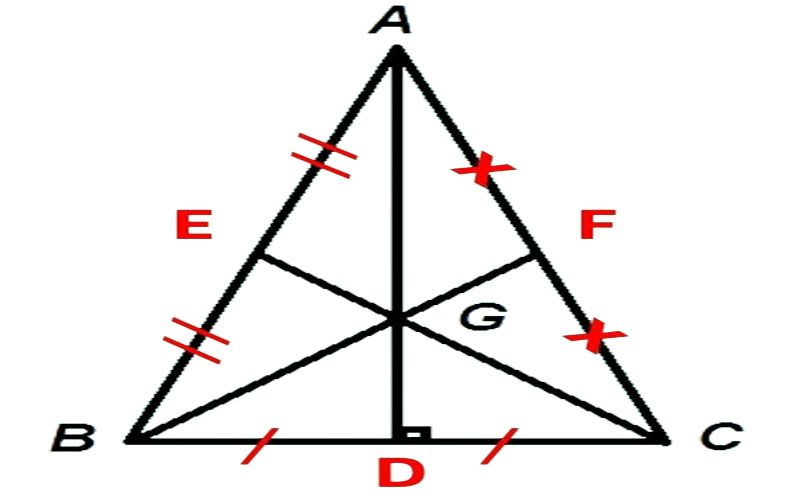
- Ví dụ: Trong tam giác ABC cân tại đỉnh A, trọng tâm là G.
- Do tam giác ABC cân tại đỉnh A, nên chúng ta có những công thức sau đây:
- Góc BAD bằng góc CAD.
- Đường trung tuyến AD vuông góc với cạnh đáy BC.
Trọng tâm của tam giác đều
- Trọng tâm của tam giác đều là một điểm duy nhất.
- Trọng tâm đồng thời là trực tâm, tâm đường tròn ngoại tiếp và nội tiếp của tam giác ABC, theo tính chất của tam giác đều.
Trọng tâm của tam giác vuông
- Trọng tâm của tam giác vuông được xác định tương tự như trọng tâm của tam giác thường.
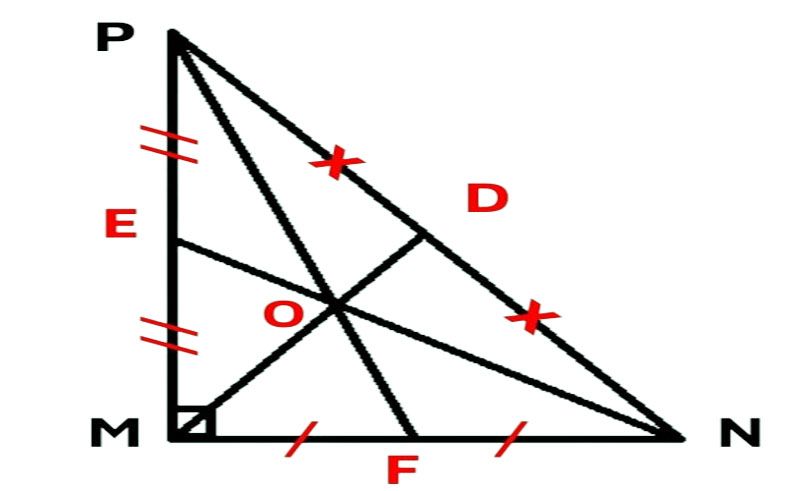
Trọng tâm của tam giác vuông cân
- Trọng tâm của tam giác vuông cân nằm trên cạnh đối diện với góc vuông và là điểm giao nhau của đường trung trực và đường trung tuyến của tam giác.
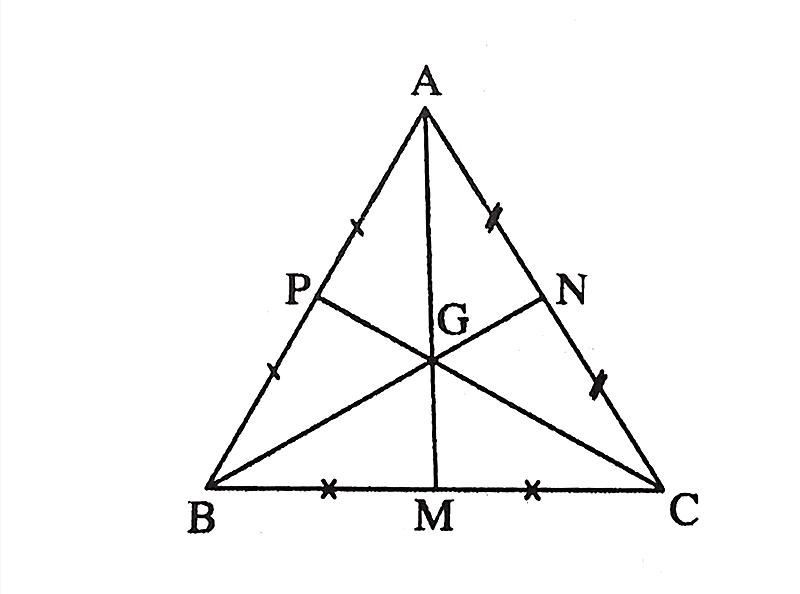
- Ví dụ: Trong tam giác ABC vuông cân tại A và I là trọng tâm, ta có các đẳng thức sau:
- AM là đường trung trực, đường trung tuyến và đường cao, nên AM vuông góc với BC.
- AB = AC => BP = CN và BN = AN = CP = AP.
Trọng tâm của tứ giác
- Trọng tâm của tứ giác là trung điểm của đoạn thẳng nối trung điểm của hai cạnh đối diện.
- Ví dụ: Cho tứ giác ABCD có trọng tâm là G, ta có công thức sau:
- Tổng vectơ GA + GB + GC + GD = 0.
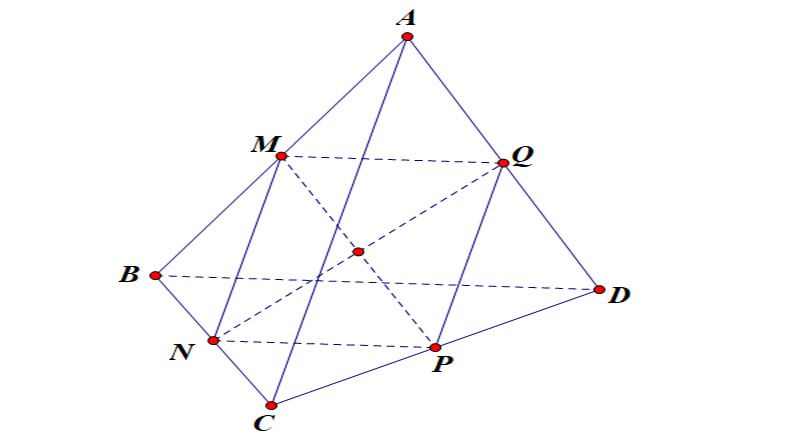
Trọng tâm của tứ diện
- Trọng tâm của tứ diện là điểm giao nhau của bốn đường thẳng nối từ đỉnh và trọng tâm của tam giác đối diện.
- Ví dụ: Trong tứ diện ABCD, trọng tâm là G.
Cách tìm trọng tâm các hình học chuẩn nhất
Cách tìm trọng tâm hình tam giác
- Cách 1: Giao điểm 3 đường trung tuyến
- Xác định trọng tâm tam giác bằng cách lấy giao điểm của ba đường trung tuyến.
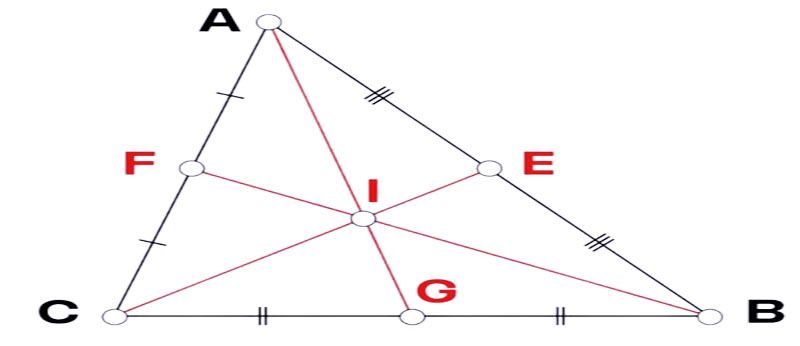
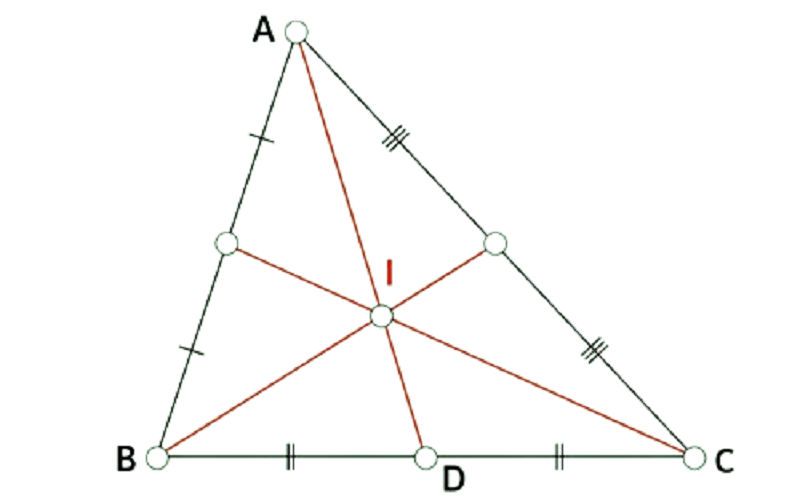
- Bước 1: Vẽ tam giác ABC và xác định trung điểm của các cạnh AB, BC, CA.
- Bước 2: Nối lần lượt các đỉnh đến trung điểm của cạnh đối diện. Nối A với G, B với F, C với E.
- Bước 3: Giao điểm I của ba đường trung tuyến là AG, BF, CE chính là trọng tâm của tam giác ABC.
- Cách 2: Tỉ lệ trên đường trung tuyến
- Xác định trọng tâm tam giác dựa trên tỉ lệ đường trung tuyến.
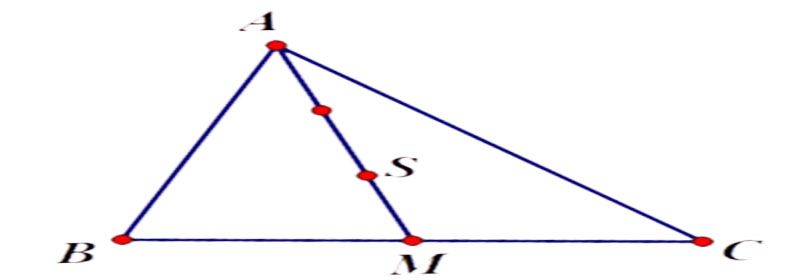
- Bước 1: Vẽ tam giác ABC và xác định trung điểm M của cạnh BC.
- Bước 2: Nối đỉnh A với trung điểm M, sau đó lấy điểm S sao cho AS = 2/3 AM.
- Theo tính chất trọng tâm tam giác, điểm S chính là trọng tâm tam giác ABC.
Cách vẽ trọng tâm của tứ diện
- Cách 1:
- Cho tứ diện ABCD. Khi đó, 3 đường thẳng nối trung điểm của 3 cặp cạnh chéo nhau đồng quy tại trung điểm mỗi đường. Điểm đó chính là trọng tâm tứ diện ABCD.
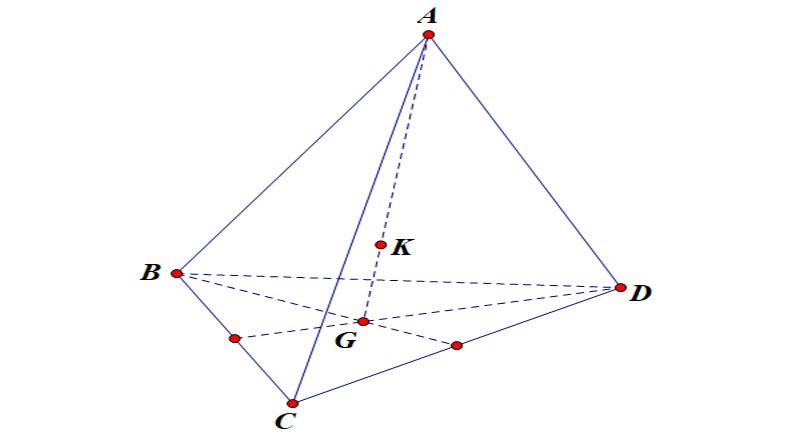
- Cách 2:
- Cho tứ diện ABCD có G là trọng tâm của tam giác BCD. Trên đoạn AG, lấy điểm K sao cho KA = 3KG. Khi đó, điểm K chính là trọng tâm tứ diện ABCD.
Một số bài tập về trọng tâm
Bài 1: Tam giác ABC có đường trung tuyến AD = 9cm và trọng tâm I. Hãy tính độ dài đoạn AI?
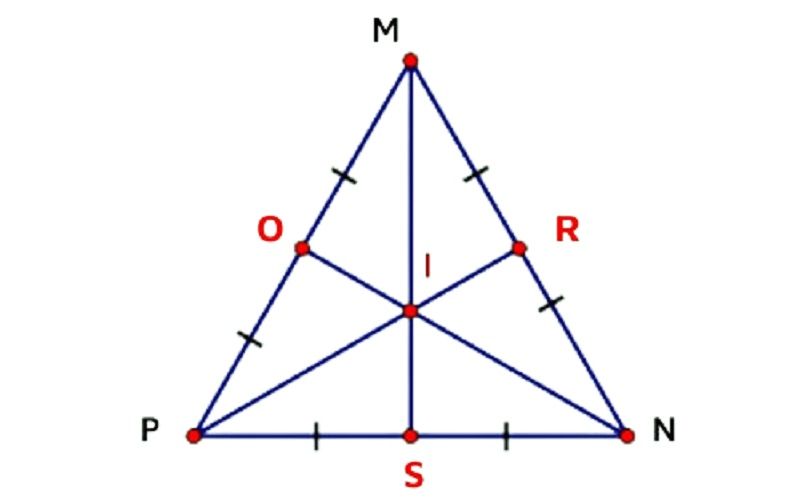
Bài 2: Cho I là trọng tâm của tam giác đều MNP. Chứng minh rằng: IM = IN = IP.
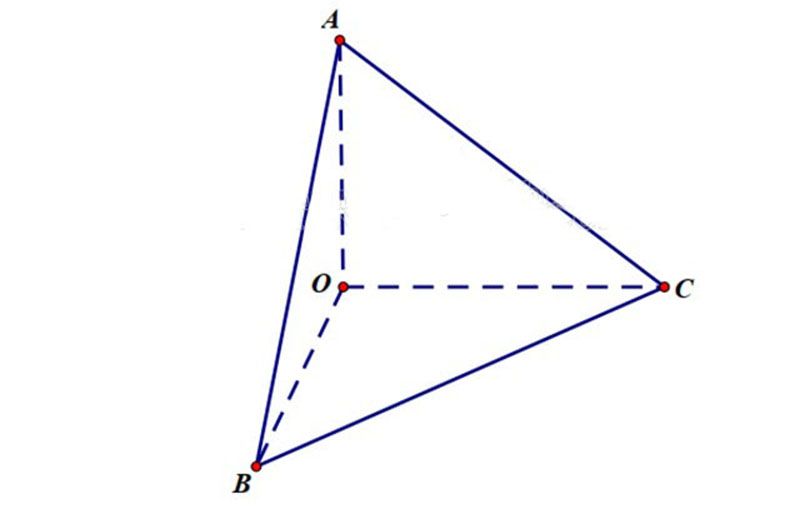
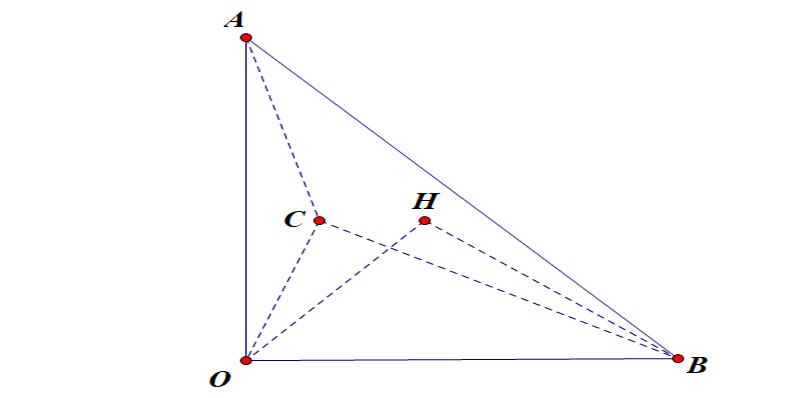
Bài 3: Cho G là trọng tâm của tứ diện vuông OABC (vuông tại O). Biết rằng OA = OB = OC = a. Tính độ dài OG.
-
Bài giải:
-
Bài 1:
- Ta có: I là trọng tâm của tam giác ABC và AD là đường trung tuyến nên AI = (2/3) AD (theo tính chất ba đường trung tuyến của tam giác).
- Do đó: AG = (2/3) x 9 = 6 (cm).
- Vậy độ dài đoạn AI là 6 cm.
-
Bài 2:
- Gọi trung điểm MN, MP, PN lần lượt là R, O, S.
- Khi đó MS, PR, NO đồng quy tại trọng tâm I.
- Ta có tam giác MNP đều, suy ra:
- MS = PR = NO (1).
- Vì I là trọng tâm của tam giác ABC, theo tính chất đường trung tuyến ta có:
- MI = 2/3 MS
- PI = 2/3 PR
- NI = 2/3 NO (2).
- Từ (1) và (2) suy ra:
- GA = GB = GC.
-
Bài 3:
-
Hy vọng rằng, với những thông tin bổ ích trên đây, bạn đã hiểu rõ hơn về khái niệm trọng tâm là gì? Cũng như cách xác định trọng tâm. Chúc bạn có một quá trình học tập tốt và áp dụng kiến thức chính xác trong quá trình học tập của mình.
