KHÁI NIỆM HÀM SỐ | Toán học phổ thông – SGK
Chào các bạn! Trong bài viết này, chúng ta sẽ cùng tìm hiểu về khái niệm hàm số trong toán học. Hàm số là một phần rất quan trọng và cơ bản trong chương trình toán học phổ thông. Bài viết sẽ giúp các bạn hiểu rõ hơn về khái niệm này và đồng thời áp dụng vào các bài tập thực hành.
Hàm số là gì?
Hàm số là một loại quan hệ giữa hai đại lượng, trong đó một đại lượng phụ thuộc vào đại lượng thay đổi. Nếu một giá trị của đại lượng thay đổi xác định chính xác một giá trị tương ứng của đại lượng phụ thuộc, thì đại lượng phụ thuộc được gọi là hàm số của đại lượng thay đổi và đại lượng thay đổi được gọi là biến số.
1. Hàm số được cho bằng hai dạng: bảng và công thức.
- Hàm số dạng bảng:
x | 0 | 1 | 2 | 3 | 4 | 5 | y | 1 | 3 | 5 | 7 | 9 | 11| - Hàm số bằng công thức (dạng tường minh):
y = f(x)Trong đó,
f(x)là biểu thức đại số với biến x.
Ví dụ:
- y = 2 : hàm hằng.
- y = 2x + 1: hàm số bậc nhất.
- y = x^2 + 2x – 1: hàm số bậc 2.
2. Tập giá trị và tập xác định.
- Tập giá trị Y là tập hợp các giá trị của hàm số y.
- Tập xác định X là tập hợp các giá trị của biến số x. Tập xác định X của hàm số y xác định.
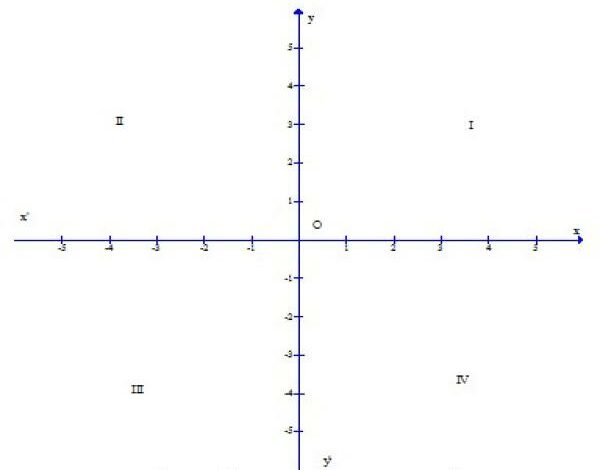
3. Đồ thị của hàm số.
- Đồ thị của hàm số y = f(x) là tập hợp các cặp giá trị tương ứng (x ; f(x)) trên mặt phẳng tọa độ.
- Ox: trục hoành.
- Oy: trục tung.
- O: gốc tọa độ.
- (I) góc phần tư thứ I, (II) góc phần tư thứ II, (III) góc phần tư thứ III, (IV) góc phần tư thứ IV.
4. Vị trí tương đối giữa điểm và đồ thị hàm số.
Cho điểm A(xA ; yA) và hàm số y = f(x) có đồ thị (c). A thuộc (c) khi yA = f(xA).
Ví dụ: A(1 ; 2) và B(-2 ; 1) có thuộc y = f(x) = x^2 + 2x – 1 (c).
Giải:
-
Tính: f(xA) = f(1) = 1^2 + 2.1 – 1 = 2 = yA
=> A thuộc (c). -
Tính: f(xB) = f(-2) = (-2)^2 + 2.(-2) – 1 = 2 = -1 ≠ yB
=> B không nằm trên (c).
5. Hàm số đồng biến và hàm số nghịch biến.
-
Định nghĩa:
- Nếu giá trị của biến tăng lên mà giá trị tương ứng của hàm số f(x) cũng tăng lên, thì hàm số y = f(x) được gọi là hàm số đồng biến trên R (gọi tắt là hàm số đồng biến).
- Nếu giá trị của biến tăng lên mà giá trị tương ứng của hàm số f(x) giảm đi, thì hàm số y = f(x) được gọi là hàm số nghịch biến trên R (gọi tắt là hàm số nghịch biến).
-
Định lí: với x1, x2 thuộc R.
- Nếu x1 < x2 mà f(x1) < f(x2) thì hàm số y = f(x) đồng biến trên R.
- Nếu x1 < x2 mà f(x1) > f(x2) thì hàm số y = f(x) nghịch biến trên R.
Ví dụ: xét hàm số y = f(x) = -2x + 1.
Giải:
- Tập xác định: R
- Cho x1, x2 thuộc R sao cho x1 < x2.
- Tính: f(x1) = -2×1 + 1; f(x2) = -2×2 + 1
- xét: f(x1) – f(x2) = (-2×1 + 1) – (-2×2 + 1) = -2×1 + 1 + 2×2 – 1 = 2(x2 – x1) > 0 (vì x2 – x1 > 0)
=> f(x1) > f(x2) vậy: hàm số nghịch biến.
BÀI TẬP SGK
BÀI 1 TRANG 44:
Cho hàm số y = f(x), tính:
- f(-2) = ?
- f(0) = ?
BÀI 7 TRANG 46:
Cho hàm số y = f(x) = 3x. Cho hai số x1, x2 thuộc R sao cho x1 < x2. Hãy chứng minh f(x1) < f(x2) rồi rút ra kết luận hàm số đồng biến trên R.
Giải:
- Tập xác định: R
- Cho hai số x1, x2 thuộc R sao cho x1 < x2= > x2 – x1 > 0
- Tính: f(x1) = 3×1 + 1; f(x2) =3×2 + 1
- xét: f(x2) – f(x1) = 3×2 – 3×1 = 3(x2 – x1) > 0 (vì x2 – x1 > 0)
=> f(x1) < f(x2) vậy: hàm số đồng biến trên R.
BÀI TẬP BỔ SUNG:
Tính giá trị của hàm số tại x = x0:
Cho hàm số y = f(x).
Bước 1. Thế giá trị của biến x bằng x0. (chổ nào có x thế bằng x0).
Bước 2. Tính y0 = f(x0).
Ví dụ minh họa: cho hàm số y = f(x) = x^3 + 2x^2 – 3x – 1 tại x = 2.
Giải:
Y0 = f(2) = 2^3 + 2.2^2 – 3.2 – 1 (bước 1).
= 9 (bước 2)
Vậy: y0 = 9
Đó là những hiểu biết cơ bản về hàm số trong toán học. Hy vọng bài viết đã giúp bạn hiểu rõ hơn về chủ đề này và có thể áp dụng vào việc giải các bài tập. Nếu bạn đang quan tâm đến ngành Y Dược và muốn tìm hiểu thêm, hãy truy cập Văn Phòng Tuyển Sinh Y Dược Hà Nội để có thêm thông tin chi tiết. Chúc các bạn thành công!


